Aprendizado de máquina é uma aplicação de inteligência artificial onde uma máquina aprende com experiências passadas (dados de entrada) e faz previsões futuras. É tipicamente dividido em três categorias: aprendizagem supervisionada, aprendizagem não supervisionada e aprendizagem por reforço.
Este artigo apresenta os conceitos básicos da teoria de machine learning, estabelecendo os conceitos e técnicas comuns envolvidos. Este post é destinado a pessoas que estão começando com machine learning, facilitando o acompanhamento dos conceitos principais e a familiarização com os conceitos básicos de machine learning.
Aprendizado de máquina explicado
Machine learning é uma aplicação de inteligência artificial na qual uma máquina aprende com experiências passadas ou dados de entrada para fazer previsões futuras. Existem três categorias comuns de machine learning: aprendizagem supervisionada, aprendizagem não supervisionada e aprendizagem por reforço.
O que é aprendizado de máquina?
Em 1959, Arthur Samuel, um cientista da computação que foi pioneiro no estudo da inteligência artificial, descreveu o aprendizado de máquina como “o estudo que dá aos computadores a capacidade de aprender sem serem explicitamente programados”.
O artigo seminal de Alan Turing introduziu um padrão de referência para demonstrar a inteligência das máquinas, de modo que uma máquina precisa ser inteligente e responsiva de uma maneira que não pode ser diferenciada da de um ser humano.
Uma definição mais técnica dada por Tom M. Mitchell Artigo de 1997: “Diz-se que um programa de computador aprende com a experiência E em relação a alguma classe de tarefas T e medida de desempenho P, se seu desempenho em tarefas em T, medido por P, melhora com a experiência E.” Por exemplo, um problema de aprendizagem de reconhecimento de caligrafia:
- Tarefa T: Reconhecer e classificar palavras escritas à mão em imagens.
- Medida de desempenho P: Porcentagem de palavras classificadas corretamente, precisão.
- Experiência de treinamento E: Um conjunto de dados de palavras escritas à mão com classificações fornecidas.
Para executar a tarefa T, o sistema aprende com o conjunto de dados fornecido. Um conjunto de dados é uma coleção de muitos exemplos. Um exemplo é uma coleção de recursos.
Tipos comuns de aprendizado de máquina
O aprendizado de máquina é geralmente categorizado em três tipos: aprendizado supervisionado, aprendizado não supervisionado e aprendizado por reforço.
Aprendizagem supervisionada
No aprendizado supervisionado, a máquina experimenta os exemplos junto com os rótulos ou alvos para cada exemplo. Os rótulos nos dados ajudam o algoritmo a correlacionar os recursos.
Duas das tarefas mais comuns de aprendizado de máquina supervisionado são classificação e regressão.
Na classificação, o modelo de aprendizagem de máquina pega dados e prevê a categoria, classe ou rótulo mais provável ao qual ele pertence com base em seus valores. Alguns exemplos de classificação incluem prever preços de ações e categorizar artigos para notícias, política ou lazer com base em seu conteúdo.
Na regressão, a máquina prevê o valor de uma variável de resposta contínua. Exemplos comuns incluem prever vendas de um novo produto ou um salário para um trabalho com base em sua descrição.
Aprendizagem não supervisionada
Quando temos dados não classificados e não rotulados, o sistema tenta descobrir padrões dos dados. Não há rótulo ou alvo fornecido para os exemplos. Uma tarefa comum é agrupar exemplos semelhantes chamados agrupamento.
Aprendizagem por reforço
Aprendizado por reforço refere-se a algoritmos orientados a metas, que aprendem como atingir um objetivo complexo (meta) ou maximizar ao longo de uma dimensão específica em muitas etapas. Este método permite que máquinas e agentes de software determinem automaticamente o comportamento ideal dentro de um contexto específico para maximizar seu desempenho. Feedback de recompensa simples é necessário para que o agente aprenda qual ação é melhor. Isso é conhecido como sinal de reforço. Por exemplo, maximizar os pontos ganhos em um jogo em muitos movimentos.
Técnicas de Aprendizado de Máquina Supervisionado
Regressão é uma técnica usada para prever o valor de variáveis de resposta (dependentes) a partir de uma ou mais variáveis preditoras (independentes).
As técnicas de regressão mais comumente usadas são regressão linear e regressão logística. Discutiremos a teoria por trás dessas duas técnicas importantes, além de explicar muitos outros conceitos importantes, como algoritmo de descida de gradiente, overfit e underfit, análise de erros, regularização, hiperparâmetros e técnicas de validação cruzada envolvidas no aprendizado de máquina.
Regressão Linear
Em problemas de regressão linear, o objetivo é prever uma variável de valor real e de um determinado padrão X. No caso da regressão linear, a saída é uma função linear da entrada. Seja ŷ seja a saída que nosso modelo prevê: ŷ=WX+b
Aqui X é um vetor ou características de um exemplo, W são os pesos ou vetores de parâmetros que determinam como cada característica afeta a previsão e b é um termo tendencioso. Então, nossa tarefa T é prever y de X. Agora, precisamos medir o desempenho P para saber o desempenho do modelo.
Para calcular o desempenho do modelo, primeiro calculamos o erro de cada exemplo i como:
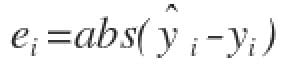
Em seguida, tomamos o valor absoluto do erro para levar em conta os valores positivos e negativos do erro. Por fim, calculamos a média de todos os erros absolutos registrados ou a soma média de todos os erros absolutos.
Erro absoluto médio (MAE) é igual à média de todos os erros absolutos:

Uma maneira mais popular de medir o desempenho do modelo é usando Erro quadrático médio (MSE). Esta é a média das diferenças quadradas entre a previsão e a observação real.
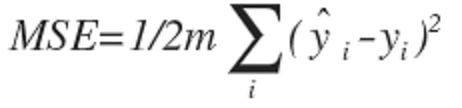
A média é reduzida à metade como uma conveniência para o cálculo da descida do gradiente, pois o termo derivado da função quadrada cancelará o meio termo.
O principal objetivo do treinamento do algoritmo de aprendizado de máquina é ajustar os pesos W para reduzir o MAE ou MSE.
Para minimizar o erro, o modelo atualiza os parâmetros do modelo W ao experimentar os exemplos do conjunto de treinamento. Esses cálculos de erro quando plotados em relação ao W também é chamado função de custo J(w)pois determina o custo/penalidade do modelo. Então, minimizar o erro também é chamado de minimizar a função de custo J.
Algoritmo de descida de gradiente:
No algoritmo de descida de gradientecomeçamos com parâmetros de modelo aleatórios e calculamos o erro para cada iteração de aprendizado, continuamos atualizando os parâmetros do modelo para nos aproximarmos dos valores que resultam em custo mínimo.
Repita até o custo mínimo:
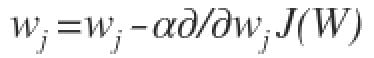
Na equação acima, estamos atualizando os parâmetros do modelo após cada iteração. O segundo termo da equação calcula a inclinação ou gradiente da curva em cada iteração.
O gradiente da função de custo é calculado como uma derivada parcial da função de custo Eu com relação a cada parâmetro do modelo wj, onde j assume o valor do número de recursos [1 to n]. αalfa, é a taxa de aprendizagem, ou quão rápido queremos nos mover em direção ao mínimo. Se α é muito grande, podemos ultrapassar. Se α é muito pequeno, significa pequenos passos de aprendizado, o que aumenta o tempo total que o modelo leva para observar todos os exemplos.
Existem três maneiras de fazer a descida do gradiente:
- Descida do gradiente em lote: Usa todas as instâncias de treinamento para atualizar os parâmetros do modelo em cada iteração.
- Descida de gradiente em minilote: Em vez de usar todos os exemplos, a descida de gradiente de mini-lote divide o conjunto de treinamento em um tamanho menor chamado lote denotado por ‘b’. Assim, um mini-lote ‘b’ é usado para atualizar os parâmetros do modelo em cada iteração.
- Descida de gradiente estocástico (SGD): Isso atualiza os parâmetros usando apenas uma única instância de treinamento em cada iteração. A instância de treinamento é geralmente selecionada aleatoriamente. Descida do gradiente estocástico é frequentemente preferível para otimizar funções de custo quando há centenas de milhares de instâncias de treinamento ou mais, pois convergirá mais rapidamente do que a descida de gradiente em lote.
Regressão Logística
Em alguns problemas a variável de resposta não é normalmente distribuído. Por exemplo, um cara ou coroa pode resultar em dois resultados: cara ou coroa. Distribuição de Bernoulli descreve a distribuição de probabilidade de uma variável aleatória que pode assumir o caso positivo com probabilidade P ou o caso negativo com probabilidade 1-P. Se a variável de resposta representa uma probabilidade, ela deve ser restringida ao intervalo {0,1}.
Na regressão logística, a variável de resposta descreve a probabilidade de que o resultado seja o caso positivo. Se a variável de resposta for igual ou exceder um limite de discriminação, a classe positiva é prevista. Caso contrário, a classe negativa é prevista.
A variável de resposta é modelada como uma função de uma combinação linear das variáveis de entrada usando a função logística.
Desde as nossas hipóteses ŷ tem que satisfazer 0 ≤ ŷ ≤ 1isso pode ser feito conectando a função logística ou função sigmóide:
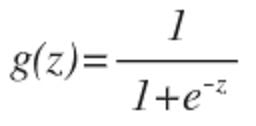
A função g(z) mapeia qualquer número real para o (0, 1) intervalo, tornando-o útil para transformar uma função de valor arbitrário em uma função mais adequada para classificação.
Agora, voltando ao nosso problema de regressão logística, vamos supor que z é uma função linear de uma única variável explicativa x. Podemos então expressar z do seguinte modo:
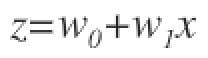
E a função logística agora pode ser escrita como:
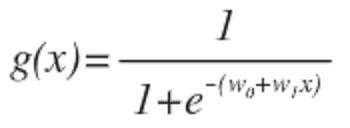
g(x) é interpretado como a probabilidade da variável dependente. g(x)=0.7nos dá uma probabilidade de 70 por cento de que nossa saída seja um. Nossa probabilidade de que nossa previsão seja zero é apenas o complemento de nossa probabilidade de que seja um. Por exemplo, se a probabilidade de que seja um é 70 por cento, então a probabilidade de que seja zero é 30 por cento.
A entrada para a função sigmóide g não precisa ser uma função linear. Pode ser um círculo ou qualquer forma.
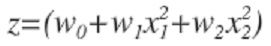
Função de Custo
Não podemos usar a mesma função de custo que usamos para regressão linear porque a função sigmoide fará com que a saída seja ondulada, causando muitos ótimos locais. Em outras palavras, não será uma função convexa.
Para garantir que a função de custo seja convexa e, portanto, garantir a convergência para o mínimo global, a função de custo é transformada usando o logaritmo da função sigmoide. A função de custo para regressão logística se parece com:


Que pode ser escrito como:
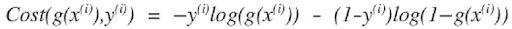
Então, a função de custo para regressão logística é:
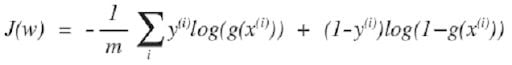
Como a função de custo é uma função convexa, podemos executar o algoritmo de descida do gradiente para encontrar o custo mínimo.
O que é Underfitting e overfitting em aprendizado de máquina?
Tentamos fazer o algoritmo de aprendizado de máquina se ajustar aos dados de entrada aumentando ou diminuindo a capacidade do modelo. Em problemas de regressão linear, aumentamos ou diminuímos o grau dos polinômios.
Considere o problema de prever y de x ∈ R. Como os dados não estão em uma linha reta, o ajuste não é muito bom.
Para aumentar a capacidade do modelo, adicionamos outro recurso adicionando o termo x² para isso. Isso produz um ajuste melhor. Mas se continuarmos fazendo isso x⁵polinômio de quinta ordem), podemos ajustar melhor os dados, mas isso não será generalizado bem para novos dados.
Subajuste
Quando o modelo tem menos recursos, ele não consegue aprender muito bem com os dados. Isso significa que o modelo tem um viés alto.
Sobreajuste
Quando o modelo tem funções complexas, ele é capaz de ajustar os dados, mas não é capaz de generalizar para prever novos dados. Este modelo tem alta variância. Existem três opções principais para abordar a questão do overfitting:
- Reduza o número de recursos: Selecione manualmente quais recursos manter. Podemos perder algumas informações importantes se jogarmos recursos fora.
- Regularização: Mantenha todos os recursos, mas reduza a magnitude dos pesos W. A regularização funciona bem quando temos muitos recursos ligeiramente úteis.
- Parada antecipada: Quando estamos treinando um algoritmo de aprendizado iterativamente, como usando gradiente descendente, podemos medir o quão bem cada iteração do modelo executa. Até um certo número de iterações, cada iteração melhora o modelo. Depois desse ponto, no entanto, a capacidade do modelo de generalizar pode enfraquecer, pois ele começa a superajustar os dados de treinamento.
Regularização em Aprendizado de Máquina
A regularização pode ser aplicada tanto à regressão linear quanto à logística, adicionando um termo de penalidade à função de erro para desencorajar os coeficientes ou pesos de atingir valores grandes.
Regressão Linear Com Regularização
O termo de penalidade mais simples assume a forma de uma soma dos quadrados de todos os coeficientes, levando a uma função de erro de regressão linear modificada:
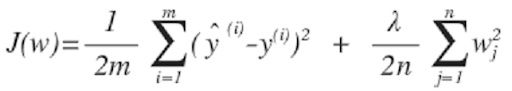
Onde lambda é nosso parâmetro de regularização.
Para minimizar o erro, usamos o algoritmo de descida de gradiente. Continuamos atualizando os parâmetros do modelo para nos aproximarmos dos valores que resultam em custo mínimo.
Em seguida, repita até a convergência, com regularização:
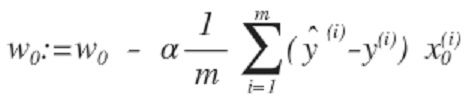
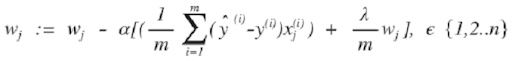
Com alguma manipulação, a equação acima também pode ser representada como:
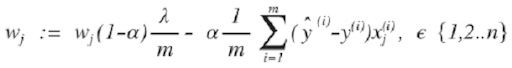
O primeiro termo na equação acima será sempre menor que um:
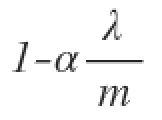
Você pode ver isso como uma redução do valor do coeficiente em alguma quantidade a cada atualização.
Regressão Logística Com Regularização
A função de custo da regressão logística com regularização é:
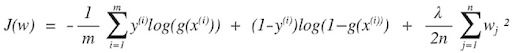
Em seguida, repita até a convergência com a regularização:
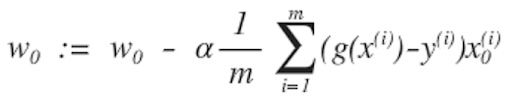
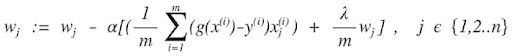
Regularização L1 e L2
O termo de regularização usado nas equações anteriores é chamado L2ou regularização de cristas.
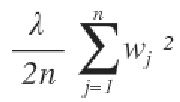
A penalidade L2 visa minimizar a magnitude quadrada dos pesos.
Existe outra regularização chamada L1, ou laço:
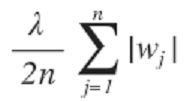
A penalidade L1 visa minimizar o valor absoluto dos pesos.
Diferença entre L1 e L2
- L2 reduz todos os coeficientes nas mesmas proporções, mas não elimina nenhum.
- L1 pode reduzir alguns coeficientes a zero, realizando assim a seleção de recursos.
Hiperparâmetros
Hiperparâmetros são parâmetros de nível superior que descrevem informações estruturais sobre um modelo que devem ser decididas antes de ajustar os parâmetros do modelo. Exemplos de hiperparâmetros que discutimos até agora incluem: Taxa de aprendizagem (alfa) e regularização (lambda).
Validação cruzada
O processo para selecionar os valores ótimos dos hiperparâmetros é chamado seleção de modelo. se reutilizarmos o mesmo dados de teste definido repetidamente durante a seleção do modelo, ele se tornará parte dos nossos dados de treinamento, e o modelo terá maior probabilidade de apresentar superajuste.
O conjunto geral de dados é dividido em três categorias:
- Conjunto de dados de treinamento.
- Conjunto de dados de validação.
- Conjunto de dados de teste.
O conjunto de treinamento é usado para ajustar os diferentes modelos, e o desempenho no conjunto de validação é então usado para a seleção do modelo. A vantagem de manter um conjunto de teste que o modelo não viu antes durante as etapas de treinamento e seleção do modelo é evitar o overfitting do modelo. O modelo é capaz de generalizar melhor para dados não vistos.
Em muitas aplicações, no entanto, o fornecimento de dados para treinamento e teste será limitado e, para construir bons modelos, desejamos usar o máximo possível dos dados disponíveis para treinamento. No entanto, se o conjunto de validação for pequeno, ele dará uma estimativa relativamente ruidosa do desempenho preditivo. Uma solução para esse dilema é usar validação cruzada.
7 etapas da validação cruzada
Estas são as etapas para selecionar hiperparâmetros usando validação cruzada K-fold:
- Divida seus dados de treinamento em
K=4partes iguais, ou “dobras”. - Escolha um conjunto de hiperparâmetros que você deseja otimizar.
- Treine seu modelo com esse conjunto de hiperparâmetros nas três primeiras dobras.
- Avalie-o na quarta dobra, ou na dobra de retenção.
- Repita as etapas (3) e (4) quatro vezes com o mesmo conjunto de hiperparâmetros, cada vez mantendo uma dobra diferente.
- Agregue o desempenho em todas as quatro dobras. Esta é sua métrica de desempenho para o conjunto de hiperparâmetros.
- Repita as etapas (2) a (6) para todos os conjuntos de hiperparâmetros que você deseja considerar.
A validação cruzada nos permite ajustar hiperparâmetros apenas com nosso conjunto de treinamento. Isso nos permite manter o conjunto de teste como um conjunto de dados verdadeiramente invisível para selecionar o modelo final.
Abordamos alguns dos principais conceitos no campo do aprendizado de máquina, começando com a definição de aprendizado de máquina e, em seguida, abordando diferentes tipos de técnicas de aprendizado de máquina. Discutimos a teoria por trás das técnicas de regressão mais comuns (linear e logística) juntamente com outros conceitos-chave do aprendizado de máquina.
























